Portals and Conservation of Energy
April 2018

I've been thinking about how to mathematically formalize portals in such a way that energy is conserved. I'll illustrate it here with a thought experiment.
Let's say we have two portals hovering above earth.
Anything that goes into one portal should come out of the same spot on the other one, maintaining its velocity. Ideally, space should still be smooth - zoom in anywhere far enough and it looks like normal, flat Euclidean space.
Assume we're in space, above earth. Newtonian gravity says there should be a force downwards, calculated from the distance r between a particle and the earth.
Notice how because of the portals, this acceleration can keep accumulating for an infinitely long time, so the particle can gain infinite amounts of energy. Obviously, this violates conservation of energy.

But why is the particle able to get infinite energy? Usually, gravity is a conservative force: potential energy is the same no matter the path one takes to get from A to B. But consider two points, each a small distance ε away from a portal. Through the portal, they're only a tiny distance of 2ε away from one another, so they should feel the same force of gravity - but they don't, since the lower point is closer to earth.

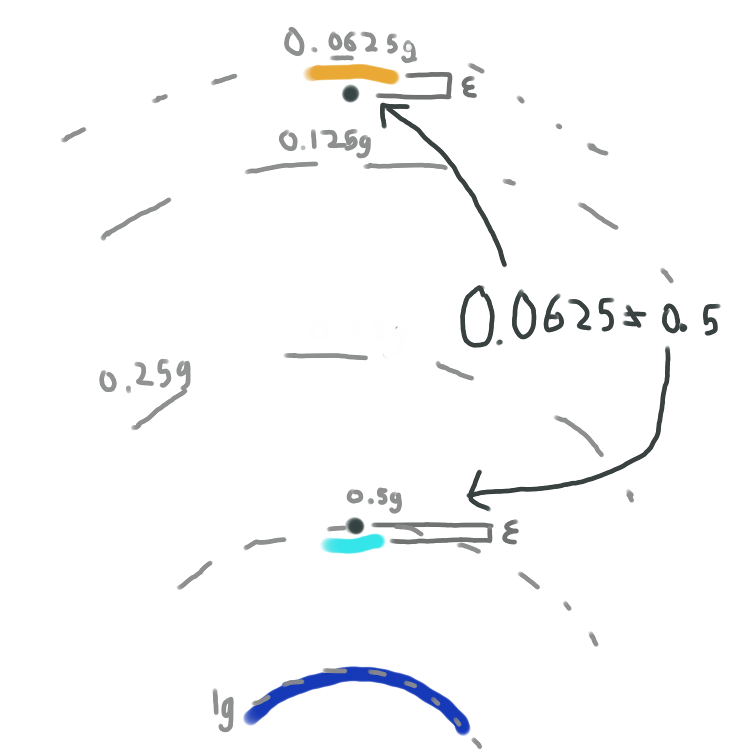
Newtonian gravity says the force F is proportional to 1/r2, where r is the distance from the point to Earth. So since the top point is farther from Earth, Newtonian physics says it experiences less gravity. Can we change how r is defined to fix the problem?

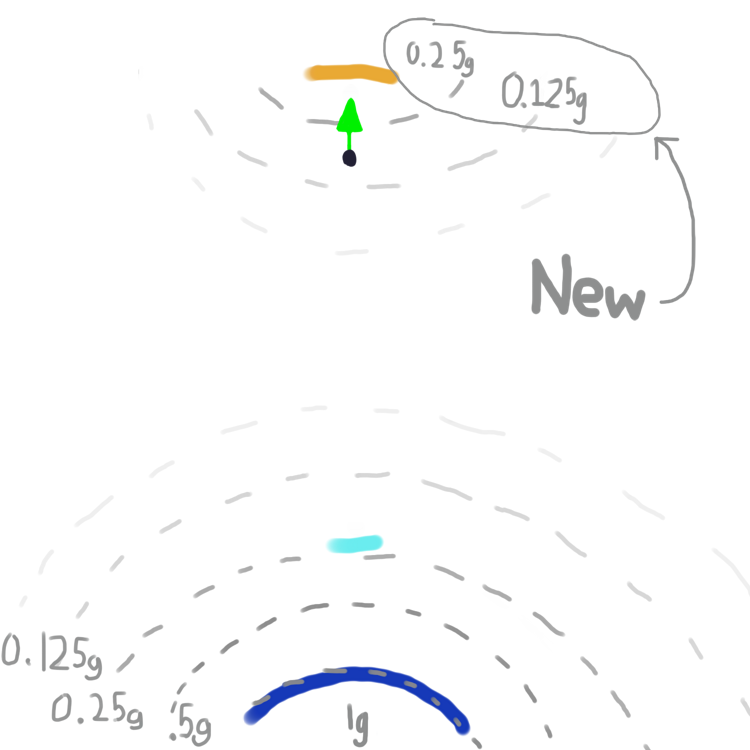
Let's let gravity flow through portals. What if we define gravity as k/r2 again; but this time, let's define r as the length of the shortest path to Earth, and the total force of gravity is the vector sum along all possible paths. This seems to fix the problem where a particle could be falling infinitely long - anything near the top portal would feel a force of gravity upwards through that portal.

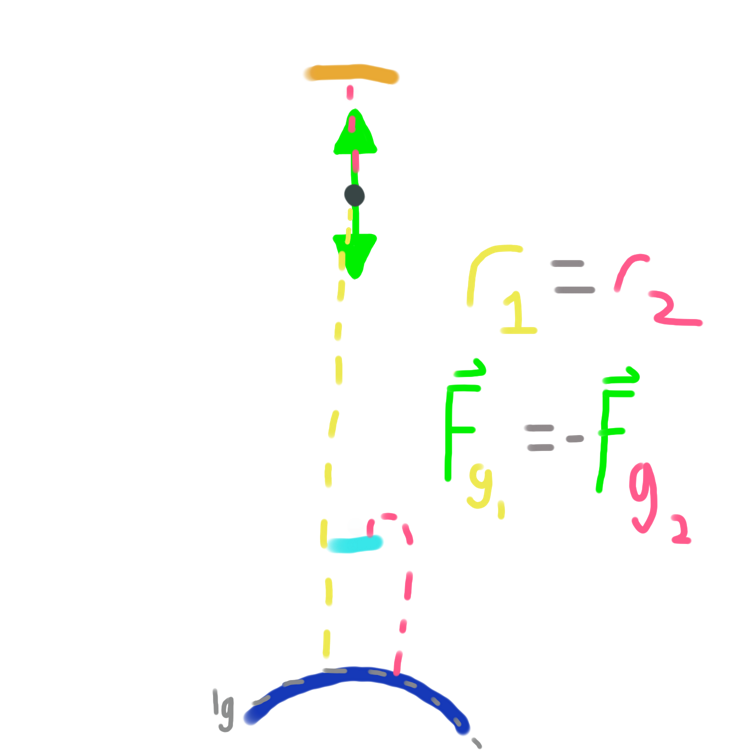
Interestingly, with this definition it's possible to levitate a particle if you carefully balance the force of gravity so it cancels itself out. It can hang there forever until it's moved.

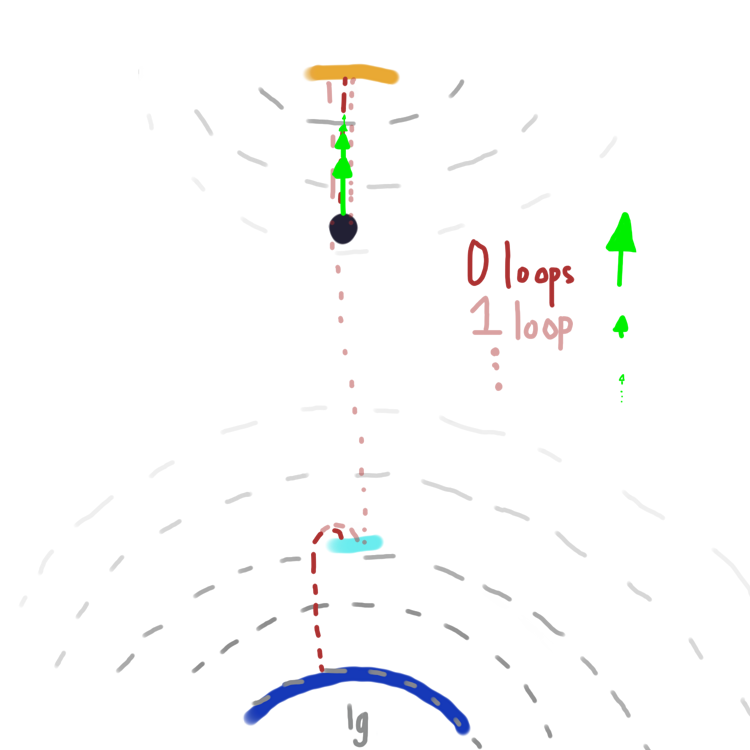
This vector summation rule also accounts for paths that take multiple trips through the portal! Let d be the distance between the two portals. If a path has distance r, each detour through a portal adds d to the initial distance to earth. The resulting force is the infinite sum
Ftotal = 1/(r)2 + 1/(r+d)2 + ... + 1/(r+nd)2
and this sum converges: no nasty infinite forces here!

There's a lot of questions to ask. How would one calculate a particle's force? These evenly-spaced lines almost remind me of waves. Could we divide space into an infinitesmal grid, give each grid square a potential, and then use something similar to the heat equation to update each square's potential based on its neighbors? In that model, maybe the portal could be represented by changing which squares are neighbors? I'm not sure!
In technical language: it seems I've done surgery on ℝ2, defined a new metric, and used something like the gradient of a function to define a conservative force. My question is: what did I just do? Is there any terminology for what I've done? Any things to learn about to figure out how better to define this maneuver? This feels very topological, and I can't have been the first one to think about vector fields on manifolds. How would I define it rigorously?

Thank you!

In technical language: it seems I've done surgery on ℝ2, defined a new metric, and used something like the gradient of a function to define a conservative force. My question is: what did I just do? Is there any terminology for what I've done? Any things to learn about to figure out how better to define this maneuver? This feels very topological, and I can't have been the first one to think about vector fields on manifolds. How would I define it rigorously?

Thank you!

Back